Reassessing the practicality of multi-party hash chains using AO primitives
With applications to threshold hash-based signatures
As part of my journey at DV Labs, one of my main research project of 2025 was to investigate the challenges of implementing threshold hash-based signatures (HBS) through multi-party computation (MPC). This is of interest to the company which develops distributed validators for Ethereum by leveraging threshold signatures (and other advanced cryptographic primitives such as distributed key generation algorithms and consensus protocols, which are not covered in this post). To date, Ethereum's consensus layer relies on the BLS signature scheme for its intrinsic aggregation feature thanks to its bilinear construction. BLS is also convenient for distributed validators as it is straightforward to turn it into a threshold variant when combined with a linear secret sharing scheme. On the other hand, distributed validators might be challenged if Ethereum ever moves away from BLS as most signature schemes do not natively support threshold constructions. Actually, we already know that Ethereum will have to break up with BLS at some point in order to meet post-quantum security, and alternatives are being considered as part of the lean Ethereum project. The preferred approach at the time of writing is a generalized variant of XMSS, a stateful HBS, instantiated with the arithmetization-oriented (AO) Poseidon2 hash function. While HBS bring many benefits to the table, support for threshold signatures is not one of them as HBS are not tailored to distributed deployments as shown by previous research. However, prior works did only evaluate standard HBS variants instantiated with traditional hash functions such as SHA2 or SHA3, and it was not clear if relying a more MPC-friendly building block would be a game changer or not, which is what I tried to answer. This blogpost gives a brief overview of this work, for more details please refer to this paper, published in IACR CiC Volume 2 (2025), Issue 4.
Related work
MPC-free approaches
When I initiated this research, there was three previous works on threshold HBS: one based on STARKs, one based on Boolean shares and another one based on MPC. I'll focus on the latter in this post but let's briefly discuss the other two alternatives' drawbacks that make MPC-based solutions appealing. The main downside of the proof-based alternative is that the signature format is not compliant with a non-threshold signature. On top of being proofs instead of "raw" signatures, threshold signatures are also significantly larger depending on the underlying proof system (between 70 and 170KB in the work mentioned above). Regarding the technique based on Boolean shares, it builds threshold signatures which are indistinguishable from non-threshold ones. However, it requires a trusted dealer and therefore cannot enjoy distributed key generations. More importantly it has huge memory requirements: a few GiB per public key is required depending on the HBS parameters. An MPC-based solution could theoretically have the best of both worlds: having compliant threshold signatures without huge memory requirements (with distributed key generation capabilities as cherry on the cake).
Hours for multi-party hash chains?
The single previous attempt of building MPC-based threshold HBS was from Cozzo and Smart who estimated the timing requirements to compute a SPHINCS+ signature over MPC, using SHA-3 as the underlying hash function, to take around 85 minutes on a local network. That definitely settled the idea that HBS and threshold signatures cannot be friend. Still, relying on an AO hash function instead of a "traditional" one could make a big difference here. Moreover, stateless HBS schemes such as SPHINCS+ require more hash calls than their stateful counterparts (e.g. XMSS). That's perfect timing as the Ethereum Foundation recently released leanSig: an XMSS-like signature with Poseidon2 as the inner primitive. All the ingredients are now in place to reassess the practicality of multi-party HBS!
Multi-Party Poseidon2
31-bit fields ftw
Poseidon2 is a generic construction in the sense that it can be instantiated with different parameters, notably the field size it operates on. While it is known to be MPC-friendly, all prior benchmarks focused on proof systems whose primary concerns are proof size and verification time. The only exception is the work from Yıldız and Maller which reports performance result for multi-party Poseidon. However they only considered a 255-bit prime field, hence it does not illustrate what can be achieved for smaller field sizes. Moreover, unlike its predecessor Poseidon, Poseidon2 supports a compression mode of operation which reduces the state size compared to instantiations with the sponge construction, decreasing the total number of multiplications and therefore leading to better MPC performance. Thefore, the first task of this work was to identify the most MPC-friendly instantiations and it appeared that they are obtained by relying on 31-bit fields such as the one defined by the KoalaBear prime defined by $2^{32} - 2^{24} + 1$. You can refer to Section 3 in the paper for more details.
Performance overview
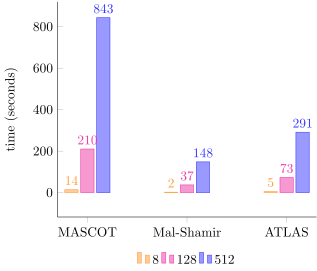
For our practical experiments, we utilized the MP-SPDZ framework and considered 3 MPC protocols with different security models as briefly summarized in the table below.
| MPC protocol | adverserial model | corruption model |
|---|---|---|
| MASCOT | active | dishonest majority |
| Malicious Shamir |
active | honest majority |
| ATLAS |
passive | honest majority |
DISCLAIMER
Note that MASCOT and Malicious Shamir rely on a statistical/correctness parameter $\kappa$ to achieve active security. In a nutshell, this parameter defines the probability for a malicious party to inject false/erroneous data during the protocol execution without being caught. It is standard to default it to 40 bits, as done in MP-SPDZ. However, $\kappa$ is bounded by the size of the field and additional calculations are required if one wants to go beyond this limit. Having $\kappa = 31$ might be acceptable in some cases but that is really application-specific. To showcase benchmark results with 40-bit satistical security, the paper also reports for MAMA, a variant of MASCOT which uses several message authentication codes (MAC) to increase the security level. Still, bear in mind that in cases where a high statistical parameter is required, it's probably worth paying the extra cost of instantiating Poseidon2 with a 64-bit prime field to avoid extra calculations on the protocol side.- 1ms one-way delay to reflect participants within the same data center or cloud region
- 10ms one-way delay to reflect geographically distributed parties within the same continent
- 100ms one-way delay to reflect intercontinental communication.
Applications to threshold HBS
Implementation strategies
Although HBS do not require to compute a single hash chains but many other ones, they are all computed from independent key components. They can therefore be evaluated in parallel without increase the number of round-trip messages in a multi-party setup. More importantly, an unique feature of HBS is their ability to precomputes signature regardless of the message to sign, at the cost of extra calculations for some signature components. Indeed nothing prevents a signer to compute in advance the entire hash chain and store all intermediate values, and that for each signature component. While it would inevitably result in "computational waste" since some signature components will very likely not require to compute the corresponding chain in its entirety, it gives the possibility to prepare many signatures in advance at the cost of some memory storage. We benchmarked this approach with the instance of leanSig used in the leanMultiSig repo, which has 68 signature components and hash chains of length 4. We also leveraged the parallelizable property of multi-party HBS to combine both implementation tricks, where the number of signatures is defined by $\sigma = \{1,2,4\}$. We kept $\sigma$ small as the ability of MP-SPDZ to compile the program with larger values was very limited. Once again this blogpost only reports results for the 10ms one-way delay network.
What performance looks like
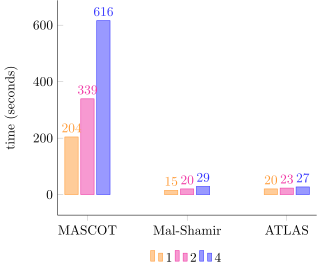
While the performance are far from being practical for MASCOT, which provides active security in the dishonest majority settings, the other two protocols are not doing so bad, especially by observing that the $\sigma$ per second metric scales as $\sigma$ increases. This parallelized precomputation trick can be of interest to practitioners as illustrated by the use case of validators on Ethereum. Indeed in leanEthereum, it is planned that each one-time key will be tied to a slot. With the current timings, validators need to sign and send their attestations within a 4-second timeframe, but it might be reduced to a single second in the future. However validators sign only once within an epoch (which currently is composed of 32 slots). Assuming a 4-second slot, validators would need to produce attestations every 2min only! Once the epoch is finished, we could imagine distributed validators precomputing signing material for their next duties during the remaining slots they don't need to contribute to. To be honest this seems a bit far-fetched, but it is interesting to note that it could theoretically satisfy real-world scenarios. Still multi-party hash chains are just one side of the coin, and other problems remains to be addressed before having a deployment-ready solution. Among those challenges, an important one is how to design a robust threshold HBS scheme (i.e. how to verify that the partial signatures are valid). We'll see if this line of research gains traction in the future!